Benford's Law seems to imply we subjectively impose preconceived ideas of order on the Universe as a whole, even as we yearn for objective explanations:
Benford's Law (which was first mentioned in 1881 by the astronomer Simon Newcomb) states that if we randomly select a number from a table of physical constants or statistical data, the probability that the first digit will be a "1" is about 0.301, rather than 0.1 as we might expect if all digits were equally likely. In general, the "law" says that the probability of the first digit being a "d" is
This implies that a number in a table of physical constants is more likely to begin with a smaller digit than a larger digit. It was published by Newcomb in a paper entitled "Note on the Frequency of Use of the Different Digits in Natural Numbers", which appeared in The American Journal of Mathematics (1881) 4, 39-40. It was re-discovered by Benford in 1938, and he published an article called "The Law of Anomalous Numbers" in Proc. Amer. Phil. Soc 78, pp 551-72.
...Although there have been many lengthy and erudite "explanations" of Benford's Law, it seems to me it can be explained with a single picture:
1---------------2---------3-------4-----5----6---7--8--9
Clearly the underlying premise of Benford's Law is that the subject population of quantities, expressed in the base 10 and more or less arbitrary units, will be fairly evenly distributed on a logarithmic scale. This is confirmed by the fact that the exponents on these constants are fairly uniformly distributed (at least over several orders of magnitude).
...Of course, we could have chosen units for our physical constants such that the leading digits were all 9's (for example), but evidently we have a natural tendency to choose units so that our numbers are evenly distributed by order of magnitude, rather than absolute value. This may be related to our basic impressions of hearing and sight (and earthquakes), since our sense impressions of loudness and brightness are logarithmic.
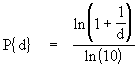
No comments:
Post a Comment